[ad_1]
Exploring the Intricate World of Cryptography: An Introduction to Cryptography Graphs
With the rise of technology and the increasing need for secure communication and data storage, the concept of cryptography has become more prominent in our daily lives. Cryptography, the science of encoding and decoding confidential information, plays a crucial role in ensuring the privacy and security of various transactions, communications, and sensitive data. Within the realm of cryptography, there exists a fascinating subfield known as cryptography graphs. This article aims to provide an introduction to cryptography graphs, exploring their significance, applications, and underlying principles.
To understand cryptography graphs, it is essential to first grasp the basics of graph theory. A graph, in the realm of mathematics, is a set of vertices or nodes interconnected by edges. These edges represent relationships or connections between the nodes. By applying graph theory to cryptography, we can create cryptographic algorithms and protocols that rely on the properties and characteristics of graphs to achieve security objectives.
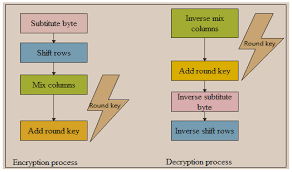
One of the fundamental concepts in cryptography graphs is the notion of a “key graph.” In traditional cryptography, a key is a sequence of characters used to encrypt and decrypt information. In a cryptographic graph, a key graph is a specific type of graph used to generate or process the cryptographic keys. This graph contains nodes that represent the characters or symbols used in the encryption process. The connections between these nodes dictate the relationships between the characters and play a vital role in the encryption process.
The structure and properties of the key graph are carefully designed to ensure the security of the cryptographic system. By manipulating the key graph’s topology, one can establish unique and complex relationships between the characters, making it challenging for unauthorized individuals to decipher the encrypted information. The selection and arrangement of nodes and edges in the graph are influenced by various cryptographic techniques and objectives, such as diffusion and confusion.

Diffusion refers to the spread of influence throughout the key graph, ensuring that any changes in the input can lead to significant changes in the encrypted output. This property prevents an attacker from deducing information about the original message by analyzing the ciphertext. On the other hand, confusion refers to the complexity and non-linearity of the relationships between the characters in the key graph. Confusion aims to obscure any patterns or correlations between the plaintext and the ciphertext, making it difficult for an adversary to discern the encryption algorithm.
Cryptography graphs find a wide range of applications in the field of secure communication and data protection. One notable application is in the design of stream ciphers, a class of encryption algorithms that operate on individual bits or characters of the plaintext. Stream ciphers utilize the key graph to generate a stream of key bits that are combined with the plaintext to produce the ciphertext. The properties of the key graph directly impact the security and efficiency of the stream cipher.
Another application of cryptography graphs is in the design of cryptographic hash functions. Hash functions are algorithms that transform variable-length inputs into fixed-size outputs, commonly referred to as hash values or message digests. Cryptographic hash functions are crucial in various security protocols, such as digital signatures and password storage. Graph-based hash functions utilize the properties of the key graph to generate unique hash values with desirable security properties, such as collision resistance and preimage resistance.
Furthermore, cryptography graphs play a significant role in the design of key exchange protocols and public-key cryptography systems. Key exchange protocols allow two parties to establish a shared secret key over an insecure channel without any prior communication. Cryptography graphs can be utilized in the generation and exchange of these secret keys, ensuring their security and the privacy of the communication. Similarly, public-key cryptography systems, such as the famous RSA algorithm, can benefit from the principles of cryptography graphs to enhance their security and efficiency.
Battle of the Crypto Giants: Binance vs. Crypto.com
In conclusion, cryptography graphs offer a fascinating avenue for exploring the intricate world of cryptography. By leveraging the properties and characteristics of graphs, cryptographic algorithms and protocols can achieve higher levels of security and privacy. Whether it is in the design of stream ciphers, hash functions, key exchange protocols, or public-key cryptography systems, cryptography graphs have proven to be an invaluable tool in safeguarding confidential information and communication. As technology evolves and new cryptographic challenges emerge, cryptography graphs will undoubtedly continue to play a crucial role in securing our digital world.
[ad_2]